M.2.1 Measurements of Postition, Velocity and Acceleration
Data Studio is used with Pasco probes to demonstrate the kinematics of one-dimensional motion.
M.2.1.1 Measurements of Postition, Velocity and Acceleration of Constant Linear Motion
Equipment: Computer, 2.2m Pasco track, Cart, Motion Sensor and Metal Slugs.
The above equipment is used in conjunction with Data Studio to measure and plot the position, velocity and acceleration of a Pasco cart as a function of time. During lecture the instructor can show quantitatively that at each instant the velocity and acceleration are the slopes of the line tangent to the position vs. time and the velocity vs. time curves respectively. Data Studio can also be used to obtain the average velocity and acceleration of the cart.

In the following Data Studio experiment, the Pasco track was propped up slightly on one end with adequate metal slugs to compensate for friction. Then the cart was given a slight push to achieve constant velocity. The motion sensor was used to measure and graph the cart's position as a function of time. The graph shows that the position changes linearly as a function of time. A linear fit to the position vs. time curve gives the slope to be 0.45 m/s. This constant value corresponds to the average and instantaneous velocities for this experiment. Furthermore, it is within experimental error of the mean of the velocity vs. time curve (0.46 m/s). Taking the slope of the velocity vs. time curve, we find that it is zero and therefore have zero acceleration -- also demonstrated experimentally.
M.2.1.2 Measurements of Postition, Velocity and Acceleration of Nonlinear Motion
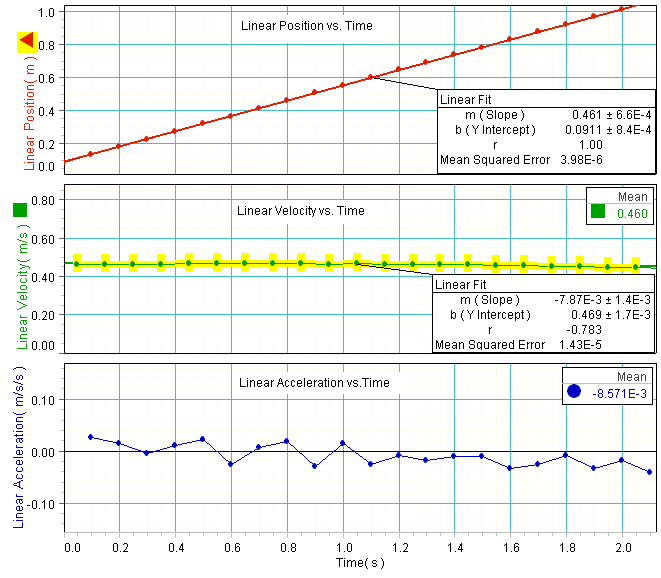
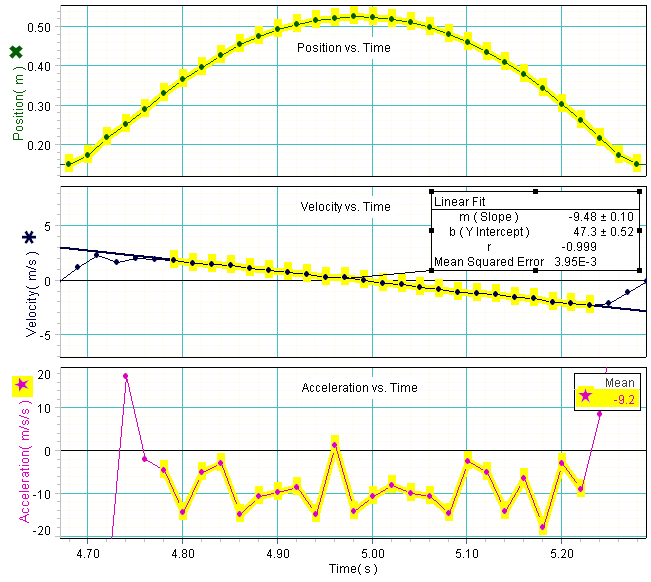
Using the motion sensor in conjunction with Data Studio and a basketball, we can study the kinematics of the ball under the influence of gravity. The ball is thrown upward above the sensor and its position is plotted as a function of time under the influence of gravity. From the graph below we see that the ball's y-position changes quadratically as a function of time. Taking the tangential slope of this curve at each point gives a plot of the ball's velocity as a function of time. The ball's velocity is a maximum as the ball is first thrown upward, zero at the ball's maximum height, and negative its maximum value when the ball returns to its initial starting position. By using Data Studio's fitting algorithm to fit the velocity vs. time plot, the slope of the linear fit is found to be -9.48 m/s/s as shown.The acceleration graph is made by taking the tangential slope of the velocity vs. time curve at each point and plotting this value as a function of time. Data Studio is then used to calculate the mean of the acceleration vs. time curve where we find the value to be -9.2 m/s/s. The values obtained by the linear fit to the velocity vs. time fit from above and the mean of the selected data points of the acceleration vs. time graph are in general agreement and close to the accepted value of gravity of 9.8 m/s/s.
All these concepts can be demonstrated quickly and efficiently during a classroom lecture.M.2.1.3 Instantaneous Velocity, Average Velocity, and Acceleration using the Air Track
Below is a sample set of demonstrations with an air track for illustrating these concepts using a clock (the "white clock") that measures the elapsed time for a glider to travel one meter and another clock (the "red clock") that measures the time for the 0.1m flag of the glider to pass a sensor at the end of the one meter interval.
1. First explain exactly what the clocks are measuring to the students. A transparency is available that can be projected during the demonstrations to remind them what is measuring what. Show them that the white clock measures the elapsed time for the glider to travel one meter by passing your hand through the start-gate, counting off "one thousand one, one thousand two, " for several seconds, and then passing your hand through the stop-gate. Then show them that the red clock measures the time for the glider flag to pass its sensor by blocking its gate with the glider flag, counting off several seconds, and removing the glider.
Then if the white clock reading is labeled T and the red clock reading is labeled t:
average velocity = 1 meter/T
instantaneous velocity = 0.1 meter/t
At some point you may wish to discuss how the exact instantaneous velocity is defined in terms of the calculus derivative by imagining the flag length to become smaller and smaller.
2. To check that everyone understands what the clocks are measuring, ask them, "If the track is level and I send a glider through the gates, what will be the relationship between the readings of the two clocks? (and then do the demo!) Answer: red clock reading = 1/10 white clock reading.
3. Now use a block to tilt the track up. Ask, "The red clock should now read (greater than, less than, the same as) 1/10 the white clock. In other words, is the instantaneous velocity at the end of one meter of acceleration (greater, less, the same) as the average velocity over the one meter distance?"
4. Now use a larger mass glider. "The clock readings should be (greater, less, the same as) before?"
5. "At what fraction of the one meter distance does the glider attain an instantaneous velocity equal to the average velocity over the one meter? In other words, where should the red sensor be placed to get red = 1/10 white with the track tilted?" (Answer: 1/4 meter)
6. You can check the measured acceleration against the tilt of the track. If the track length is L and it is tilted height h,
acceleration = a = g sin q = gh/L
Then from the white clock, a = 2 meters/t2 a = 2 meters/T 2
and from the red clock, a = (0.1m/t)2/2m = 0.005 meters/t2