Here we introduce the SPMS method.
Though this method is described in Miura and Kida[9]
and Kida and Miura[8], we summarize how to implement this
method in order to explain what we are doing to extract vortex
structures in turbulence and how to visualize them.
The essence of this method is explained by the following four processes.
First, we find planes on which the pressure takes sectional-minima
because we expect that swirling motions of fluids tend to reduce
the pressure inside swirling motions.
(It should be noted here that existence of sectional-pressure-minimum
is neither the necessary condition nor the sufficient condition for
swirling motions to exist there.)
This procedure is achieved by considering the hessian of the pressure,
.
Suppose that the three real eigenvalues of the pressure hessian is
given as 
.
By using these three eigenvalues, the pressure can be written as
up to the second order where the coordinate axis of 
s are given
by the three eigenvectors of the pressure hessian.
Then, find grid points 
such that
because the pressure takes a local minimum
on a plane perpendicular to the third eigenvector associated with the
eigenvalue 
.
Thus we expect that a line l which is parallel to the third eigenvector
and drawn on 
is a central axis of the vortex.
Hereafter, we concentrate on points 
which are
foot-points of vertical lines dropped from grid points 
to corresponding lines l.
Next, choose 
s (simply called ``candidates'' of skeletons) which
are located in the neighborhood of s so that candidates far from
s may be contaminated by various numerical errors and give
zig-zag- or inappropriately connected skeletons.
In other words, it is sufficient to adopt s neighboring to
s to construct skeletons.
This condition is expressed by an inequality
.
Then we impose the swirl condition on the planes of the
pressure-minimum so that points of the sectional-minimum without
swirling motions are removed from the candidates.
Project a flow field on a plane perpendicular to the third eigenvector
and linearize the velocity field around 
.
Then we have
on the frame moving with the velocity at .
Then a condition for the flow to be elliptic or spiral on this plane
is given by the negative of the discriminant of 
matrix A:
This discriminant is expressed by quantities of the original
-coordinate system as
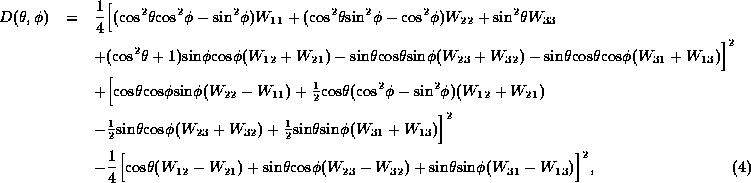
where angles 
, which give a rotational transform from the
-coordinate system to 
-coordinate system,
are determined by utilizing the third eigenvalue of the pressure hessian.
By imposing 
on candidates of skeletons, we have
less number of candidates of skeletons.
At last, we have a set of candidates of skeletons 
which are relatively less contaminated by numerical errors and accompanied
with swirling motions.
By connecting s, we have skeletons which represent central axes of
vortices.
Once we have obtained skeletons of swirling vortices, we can define
vortex cores without ambiguity.
These cores are obtained by looking for the negative discriminant
around the skeletons where are
given by the third eigenvectors on the skeletons.
We here put short comment on visualization of vortex cores.
The vortex cores can be expressed in the three-dimensional graphics
easily by using polygons.
First, we find outer boundary of a cross-section of the vortex core.
If we have two neighboring cross-sections, we put polygons (in many
cases they are triangles) to cover the region between these two
cross-sections.
Similar representation of skeletons and vortex cores has been proposed
by Banks and Singer[10], although there are some ambiguity
in their definition of skeletons and cores.
In the next section, we apply the SPMS method to extract vortical structures of turbulence and analyze them.
