Figure 1

A case in point is the propagation of action potentials in the heart, the fundamental electrical wave which is responsible for the heart's contraction as it pumps blood. This wave is governed not by hyperbolic equations, but by a diffusion equation with nonlinear terms, representing the excitability of the medium. The phase velocity, for example, is critically dependent on the rise-time of the leading edge of the wave, which in turn must be followed with timesteps on the order of microseconds. On the other hand, the remainder of the wave evolves on timescales on the order of tens to thousands of milliseconds. To model a system of any reasonable spatial size, in two or perhaps even three dimensions, an algorithm must be devised which takes appropriately small timesteps in the vinicity of the leading edge of the wave, and large timesteps everywhere else. I am currently experimenting with such an algorithm, which bases the timestep size on the estimated accuracy of the membrane voltage and the ion channel gating quantity responsible for leading edge's fast timescale. Values for the membrane voltage in adjacent cells, needed for the diffusion term, are calculated by linear interpolating using existing values. Bookkeeping is maintained through the use of an object-oriented binary tree.

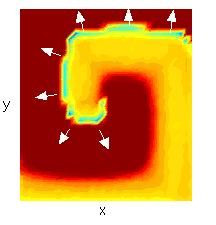
Another topic of interest which may require new numerical methods is that of cardiac spiral waves, appropriately named, as illustrated in Figure 1. These are action potential wave patterns which, unlike the normal wave pattern of the heart, pump little or no blood. They may be manifested clinically as various types of tachycardia or fibrillation, which are often fatal. There is an ongoing controversy as to whether these waves exist in the clinical setting. The key to the behavior of these waves lies in the so-called spiral core, the center of the spiral in Figure 1. In this region, no clear action potentials exist. The dynamics of the core are therefore very complicated, and in all probability determine whether the core is stable, whether it wanders or is fixed, and whether it is suspectable to breakup into two or more spiral waves.

Figure 2

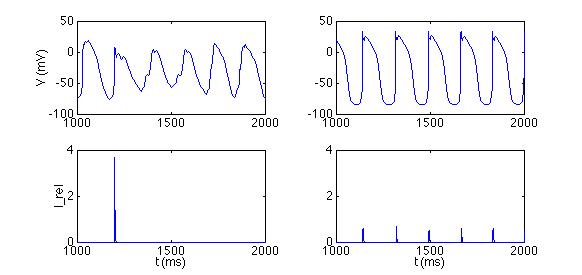
The dynamics of the core are likely to depend on a mechanism called calcium-induced calcium release (private communication, Y. Rudy), among other factors. Cardiac muscle is known to release large amounts of calcium internally to each cell, when the change in calcium over a particular time interval exceeds a certain threshold. The bursty nature of this release in the core region (Figure 2, lower left, showing the calcium release vs. time) leads to very complicated dynamics (Figure 2, upper left, showing the core voltage vs. time). In comparison, calcium release occurs more predictably, at the beginning of each action potential, away from the spiral core (Figure 2, right panels). The relevant equations depend not only on the current state of the cell, but also on a particular integral of past time behavior. The numerical question to be asked, then, is how one applies methods any more complicated than forward Euler to such a situation.

Spiral waves can also be studied numerically by representing the behavior of the wave as a dynamical system. Imagine sitting at fixed location close to the spiral core. If the core is stable, then you would see the same pattern each time the action potential wave came around. A bifurcation or more complicated instability in the core would be manifested as an alternating pattern or something more involved. This situation may be modeled as a mapping which defines chosen features of a given action potential as functions of these same features for previous action potentials. In our model, we define two time integrals of the action potential as our dynamical variables and define the mapping using data from experiments. We then demonstrate the mapping reproduces the bifurcation behavior observed in the experiment.

For more information, see:

http://reentry.cwru.edu/otani/cv/comput_biology_abs.html