To derive the upper spin limit for the top and some of the other dynamics, we need
to go back to the equations of motion.
While our computer solution of the equations of motion keeps terms to second order,
the upper spin frequency condition can be derived from the linearized equations.
We write equations (1) and (2) in terms of our field expansion. For the z-component
we have
The term in the brackets is zero at the levitation point. The top is trapped
in z and oscillates at a frequency
Defining 
so that 
changes
sign when 
changes sign,
the other equations are
We change to complex variables 
and
u=x+iy and solve by substituting 
and
.
The result is a cubic equation for 
. The condition that the motion
be bounded is that all three roots of the cubic are real. From this the
condition for
stability can be derived and is 
where
The function 
is nearly constant and ranges between 0.77 and 1.
It is approximated by the simpler function
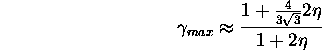
within 0.36%.
These relations determine the upper spin limit for stable operation. The absolute
upper spin limit, setting 
, is
The
analytical results have been confirmed by computer simulation of the complete
equations (see appendix 2) and by experiment within 20%.