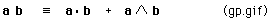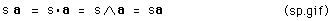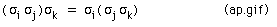Geometric Algebra

A Picture Interpretation of the Paper
"Imaginary Numbers are not Real - the Geometric Algebra of Spacetime"
by Stephen Gull, Anthony Lasenby and Chris Doran
http://www.mrao.cam.ac.uk/~clifford/introduction/intro/intro.html

sclr.gif: A scalar has no sense of direction associated with it. It is represented by a point.

vctr.gif: A vector has its traditional properties. Its sense is its direction.

bivctr.gif: The outer product of two vectors is a bivector. It is an emergent attribute confined to the space of the two vectors. The kinked arrow marks the 'sense' of the bivector = a sense of rotation in the plane.
Bivector = grade 2 vector.

snses.gif: Bivectors of the same magnitude but opposite senses.

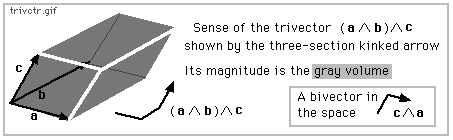trivctr.gif: The outer product of three vectors is a trivector. This 3-D space contains scalars, vectors, bivectors and trivectors.

The Three Essential Ingredients of the GA Structure

The rule for the GEOMETRIC PRODUCT of two vectors

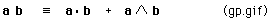The rule for multiplication by a SCALAR: inner, outer and geometric PRODUCTS ARE EQUAL. The vector is extended in length by the factor, s.

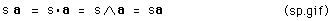The ASSOCIATIVE PROPERTY OF GEOMETRIC PRODUCT multiplication of orthonormal basis vectors.

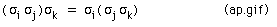
Question: This property is not obvious to me. How is this associative property proved? Is this an axiom imposed on the structure? If so how do we know it is consistent with the structure?
Answer by Richard Harke: Hestenes and Szobcyk make associativity one of the axioms from which the other properties can be derived. See his web page for a somewhat more advanced introduction. (downloadable in postscript)

January 1998
Marvin Chester
e-mail: chester@physics.ucla.edu

Return to Site Contents
9'05-