Neutrinos for Submarine Communications
by Silja
Haapanen
Physics 199
Spring 2003
1.Introduction
The purpose of this study was to inspect the possibility of using neutrinos for communications for military submarines. The basic design of this idea is based on the Navy's current submarine communications system, specifically the Extremely Low Frequency (ELF) Radio Communications; the main difference is the use of neutrinos in place of radio waves. The ELF Radio Communications program is a fixed, shore-based transmitter- a 222-km dipole antenna located in Wisconsin. Simple, one-sided commands can be transmitted to submarines operating in certain range of depths. The transmission frequency is 40-80 Hz; this is a great improvement from the earlier communications systems which used higher radio frequencies. The longer wavelengths can better penetrate the ocean, and there is an overlap between the operational depth of the submarines and the depth at which messages can be received. In other words, the submarines do not have to surface just to receive communications.
Neutrinos have many properties that would make them superior even to the extremely low radio frequencies. Because neutrinos are nearly unaffected by matter, a neutrino beam could traverse directly through the earth from the transmission site to the submarine. A directional beam would allow confidential information to be passed only to the intended recipient. Neutrino communications would also be totally jam-proof. As an additional benefit, a neutrino message could be received in the deepest of waters, leaving a submarine less vulnerable to enemy attacks.
2.Transmission
The neutrino beam would be produced by an accelerator, preferably built at some well- protected location in the U.S..
The neutrinos would be produced
via pion decay, similarily to the method employed by current accelerator beam
neutrino experiments. Colliding a proton beam with a target produces positive
pions, π+. Because the
pions are electrically charged, they can be focused by using a magnetic
field (Figure 1). The field is created by devices called
magnetic horns. The horns are two coaxial barrels made out of electrically
conductive material and use a large current in the order of 200 kA; they produce
a toroidal magnetic field in the region between the barrels. The pions will be focused into a highly
parallel beam. They will then decay to a muon and a muon neutrino, and the muon
in turn decays into a positron, neutrino and an antineutrino:
π+→µ++υ
µ
(1)
µ+→e++υµ
+υe
The end result is a highly directional beam of mostly muon neutrinos. The beam could be turned off and on rapidly; this could be used as a means of modulation. It would be fairly easy to produce a Morse code- type binary code.
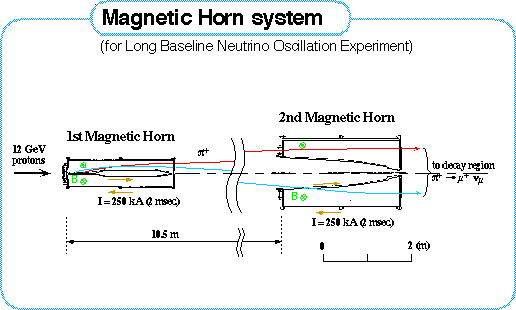
Figure 1. The magnetic horn system of the K2K experiment.
3. Long Beamline Neutrino Experiments
The concept of a neutrino beam traversing through long distances of earth is already being implemented for a purpose quite different from underwater communications. Very long beamline neutrino experiments, such an K2K and MINOS, are using accelerator- created beams for neutrino research; specifically, to increase understanding of neutrino oscillation. A well- understood and controlled neutrino source, set at a fixed distance from a detector, will enable a more accurate measurement of neutrino oscillation parameters.
K2K is a Japanese experiment whose name stands for " KEK to Kamiokande" , the locations of the accelerator and the detector, respectively. The distance between them is 250 kilometers. KEK is a 12GeV proton synchrotron accelerator. The neutrino beam is produced by pion decay as described above; the pion decay pipe is 200 meters long, and the average energy of resultant neutrinos is 1.3 GeV.
The Kamiokande detector is a liquid scintillator Cherenkov detector which was originally built for observing proton decay. It later discovered that the atmospheric neutrino deficit problem can be explained by neutrino oscillations. Kamiokande has taken on a new assignment as a detector for accelerator- created neutrinos. Its detection volume is 22 kilotons, or 22,000,000 kilograms.
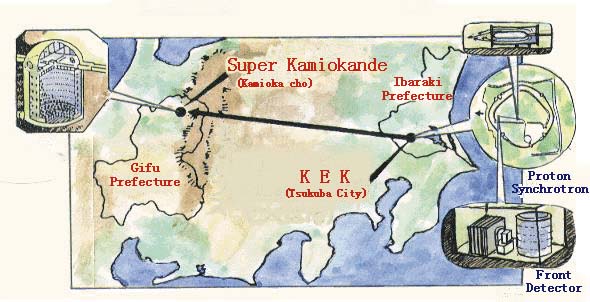
Figure 2. The K2K experiment
Another interesting long baseline experiment is MINOS (Main Injector Neutrino Oscillation Search). Its 731-kilometer baseline runs from Fermilab to Soudan Mine in northern Minnesota. At MINOS, the pion decay region is 675 meters long. MINOS features an adjustable magnetic horn system, which can select 3 different neutrino energy ranges: 3, 6, and 15 GeV. A look at MINOS' 5.4 kiloton detector event rates gives an idea just how challenging it is to detect neutrinos: the charged current event rates are 10,000 events/year for the 15GeV neutrinos, 5,000/year for the 6GeV and a modest 700/year for the 3GeV neutrinos.
4.Receiving
Detection of the messages would happen via Cherenkov radiation, and the detection medium would be the water around the submarine. The submarine would be equipped with an array of photomultiplier tubes. The phototubes would pick up the Cherenkov light that is produced when a neutrino collides with a nucleon in the target volume; a pair of electrons created in the collision travel through water at a speed faster than light speed in the medium.
The transparency of sea water peaks at the blue wavelength of visible light.
Cherenkov radiation can be detected to about 100 meters from the source.
The 'Ohio' class submarine, which is used to carry both ballistic and guided missiles, is 171 meters in length. A reasonable phototube array would be about 100 meters long, an extension to be dragged behind the submarine.
The detection volume would therefore be a cylinder with 100m radius and 100m length. This translates to π×109 liters, or p ´106 tons, of sea water. Assuming that sea water mostly consists of H2O, using the conversions 1 liter/kilogram and 18 grams/mole, the number of target nucleons in this volume is 1.9´1035 nucleons.
5.Event Frequency
Total number of events can be calculated from the equation
N = (n)(σ)(I)
(2)
where n = number of target nucleons in the target volume
σ = beam particle cross-section
I = beam intensity (flux/area)
The beam divergence and the distance between the transmitter and the submarine will affect the intensity. The distance would, for practical use, be of the order of 1000 kilometers or 106 meters. The number used for the calculations in this study is 5000 kilometers.
The beam divergence is decided by the pion momentum. The pions will have longitudinal and transverse momentum components. The transverse component is always of the order 0.5GeV, regardless of the magnitude of the longitudinal component. The beam divergence angle is given by
tan(θ) = pt/pl (3)
where pt = transverse pion momentum
pl = longitudinal pion momentum
The larger the total momentum of the pions, the smaller the spread in the beam. For pions with a longitudinal momentum of 50 GeV, the beam, at a distance of 5000 kilometers from the source, has spread to a radius of about 158 kilometers. For longitudinal momentum of 100 GeV, the spreading radius would only be about 79 kilometers.
The neutrino cross section/energy versus energy is linear and has a value 0.67x10-38 cm2/GeV. A neutrino beam of 10GeV therefore has a cross-section of 6.7x10-29cm2
The intensity has to be taken per area; for (3) to be dimensionally correct, the intensity is given as (particles)/(second)(cm2).
The area is given by
A = p D2 sin2q
(4)
where q = beam divergence angle
D sinq = radius of the incidence area.
For the case where the pions have 50GeV longitudinal momentum, A = 3.1x1017cm2.
Inserting this value into (2), together with the known values of s and n, gives
N = d(flux)
(5)
where d = (n)(s)/(A), with the numerical value (1.9´1035) (6.7´10-29) (3.1´10-17) =3.9´10-10 .
From this one can easily see that to have the possibility to detect even just one event per second, a flux in the order of 1010 amperes is needed!
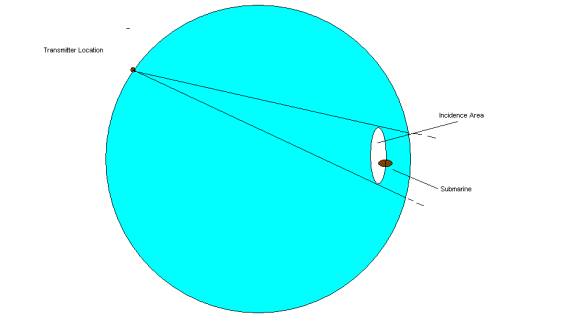
Figure 3. The geometry of neutrino beam communications. The sizes are, of course, very exaggerated...
6.Pion Beam Deflection
In order to point the neutrino beam towards the desired direction (i.e. the submarine), the pion beam could be deflected by using a magnetic field. The magnetic force on a charged particle in an external magnetic field is given by
FB = qnAL(v
´ Bo)
(6)
where q = charge of the particle
n = number of particles in the volume element
A = cross-sectional area of beam
L = length of magnetic field region
v = velocity of the particle
Bo = magnetic field.
Or, more simply for one particle,
FB = q(v
´ Bo)
(7)
A charged particle moving in a magnetic field will follow a helical path. Newton's 2nd Law can then be written as
mv2/r = qvBo (8)
and
r = mv/qBo
(9)
These are familiar cyclotron motion equations, where r = radius of curvature of the particle's path and m = the particle's mass.
While the pion is inside the region of the magnetic field, it will travel a helical arc length S.
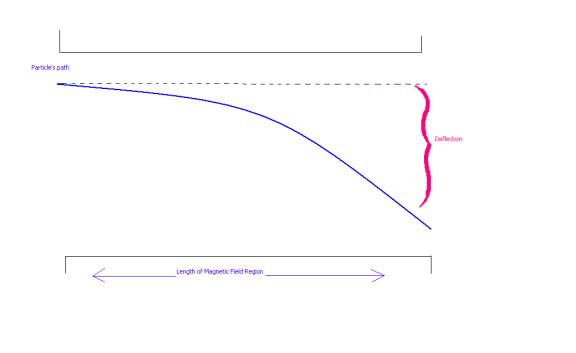
Figure 4. A particle in a magnetic field
The purple line represents the path of the particle, S. The magenta line is the amount by which a particle gets deflected in the transverse direction. The particle is deflected by angle a; it can easily be seen that if we call length of the magnetic field L , and the transverse displacement D,
L tan a= D (10)
From (8) and some trigonometry,
D =
(mv/qB)(1-cosa)
(11)
The strength of the
magnetic field is given by
Bo = mv (1-cosa)/q(D-Ltana)
(12)
where
m=Mass of pion = 139.5MeV= 2.48315x10-28kg
q = Charge of pion = 1.6022x10-19C
v=pion
velocity
D=transverse
displacement
L= length of
magnetic field region = 100m
If pion velocity is
of the order of 1:10c, deflecting its path by 30 degrees over 100 meters would
require 0.8 ´10-2 T; in other words, 0.8 T per
meter.
7.Conclusions
Neutrino communications may appear at first a tempting and interesting alternative to radio transmission. However, the very aspects which give the neutrino its benefits over electromagnetic waves, also cause the idea to fail. Neutrinos hardly interact with matter; although it would be beneficial for the military to be able to send communications to their submarines right through the earth and to the deepest places of the oceans, the difficulty of receiving the message is where the idea falls apart. Merely creating a beam with enough intensity to reliably transfer information is an impossible task. There are also a host of other problems. Bending the pion beam requires a magnetic field and only works for certain angles; aiming the beam in various directions would require the entire accelerator apparatus to be turned around in some manner. This would be very difficult, if not impossible. Smaller practical problems arise from the phototube array. Dragging a 100- meter extension behind a submarine would not only slow down the vessel and increase its energy consumption, but electrical activity from the phototubes would be highly visible to any enemy. Therefore, even if the phototube array was shielded only to be deployed when an incoming message is expected, it would not be much of an improvement from the times when a submarine had to surface in order to receive communications.
Regardless of the seeming appeal of the concept, neutrinos as a means for communications appears impossible in practice. It would take nothing less than some type of a technological revolution to make it reality; until then, neutrino communications will remain the stuff of science fiction.
8. References
Perkins, Donald H.: High Energy Physics, 4th edition
Thanks to Professor Jay
Hauser and Professor David Saltzberg of the Physics Department at the University
of California, Los Angeles.