
(The following is intended to be copied and given to your students to instruct them while they do the activities. No doubt the wording and our use of language is inappropriate for your particular grade level. We would be very interested in having teachers tell us how to revise the language in these discussions to make them more appropriate for different specific grade levels.)
Applying Forces, doing Work and developing Power.
Applying Forces:
Force is a push or a pull and many forces are acting on you all of the time. Usually you don't even realize that the force of gravity is acting on you, but it is, all of the time. If you are falling, it's pretty obvious that something is pulling you down but even if you are standing on the floor, perfectly still, the force of gravity is still pulling you down. And the really hard thing to understand is, if you are standing perfectly still on the floor, the floor is pushing up on you just as hard as gravity is pulling you down! Let's see if we can understand this by doing some simple experiments with rubber bands.
Pulling forces and rubber bands. Slowly stretch a rubber band and think about what you are doing. Most people use two hands placed at opposite ends of the rubber band and pull with each hand away from each other. This means there are two pulling forces acting on the rubber band in opposite directions. Now try to stretch the rubber band by using one hand and by grabbing the rubber band at only one place. We know it's possible to stretch the rubber band with one hand using your thumb and finger at two different places but can you figure out a way to stretch the rubber band by applying the force at only one place? If you hooked the rubber band over something to stretch it, is there only one force acting at only one place?

Two people can stretch a rubber band by pulling on either end, one person can stretch a rubber band by pulling at either end. When you hook a rubber band over something like the leg of a chair, does the chair pull when you pull the other way on the rubber band? (Think hard about this, one of the smartest people who ever lived finally figured this out and before he did, no one understood it.)
Pushing forces and the paper binder clip. You must pull to stretch a rubber band but forces are just as often exerted by pushing. Using your thumb and index finger, push inward on the "ears" of the binder clip until it opens. Now open it by using the thumbs on each of your two hands. Notice, every time you open the clip, you must push in the opposite direction in two different places. Now try to open the clip by holding only one of the "ears". If you did this by pushing with one hand while the other "ear" was pressed against a table or a wall, are you really pushing on the clip in only one place?
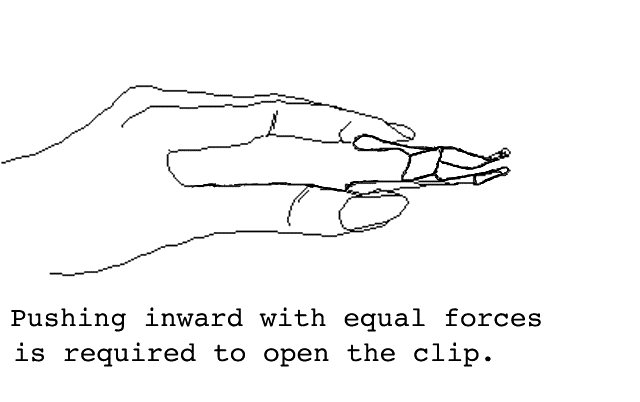
Two people who are able to cooperate can open the clip by pushing together on each of the two "ears". Careful experimentation should reveal that each of the two people must push equally hard in the opposite direction. However, you should find that it is impossible to open the clip using a single force on only one of the "ears".

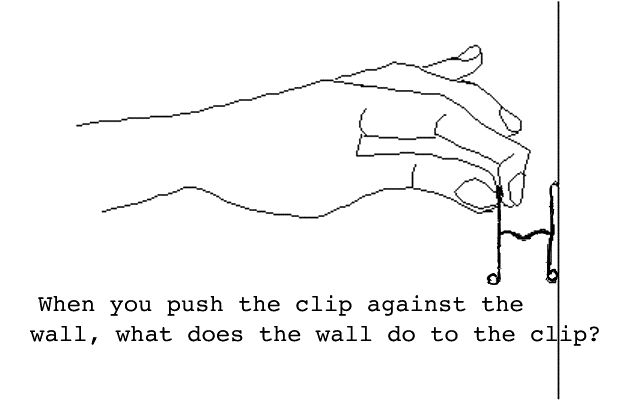
Think hard about this. Most people think that walls and tables can't push but what is the difference between having a friend pushing on one side of the clip or having a wall push on one side of the clip? If you understand this, you will finally understand that whenever you push on something, it will always push back with an equal force.
Doing Work:
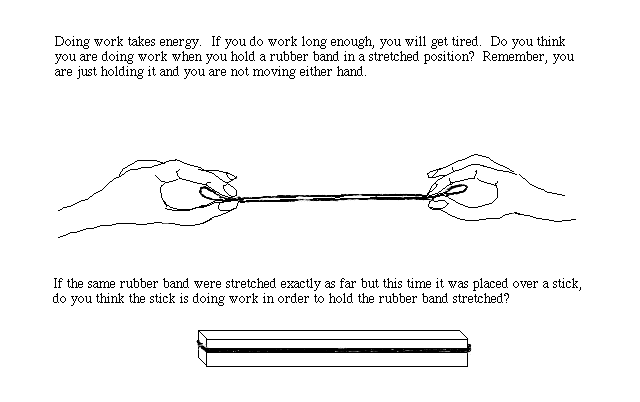
When you do work, real work, you get tired. If you are smart, however, just exerting forces, shouldn't get you tired. Does holding a rubber band stretched get you tired? If someone told you to hold a rubber band stretched for a day, you might get tired but not because you did any work. What if you used a stick or a pencil to hold the rubber band stretched? Does the stick get tired? Just applying a force isn't work, only when you apply a force through a distance, do you do work.
Imagine you have a friend sitting in a wagon and you are going to pretend that you are a horse and pull the wagon. You will pull the wagon with a special bunjy cord puller so you can always apply the same force, whether you are moving or standing still.
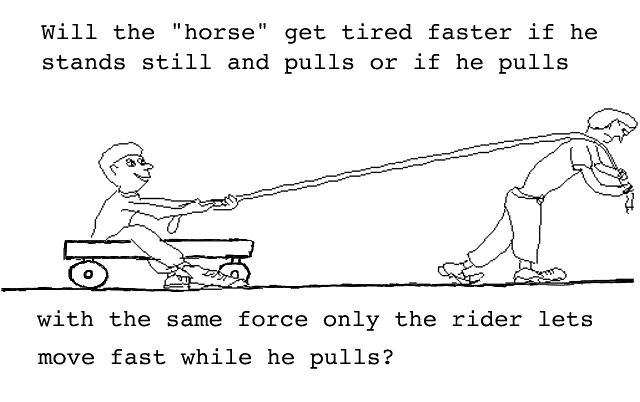
Your friend in the wagon puts his feet on the ground and won't let you move. You pull the cord so that the nylon string just touches the bunjy cord. How long do you think you could hold the cord tight before you get tired? (Here you are applying a force but you are not doing any work.) Now your friend in the wagon lets his feet slide so you can pull just as hard as before only now you are pulling and moving too. How long do you think you can keep this up until you get tired? Now you are doing work and this takes energy. If you keep this up for a very long distance, you would probably get winded. If your friend lets you move very fast and you still pull with the same force, you will get very winded. When you just pull without moving, you are exerting a force but you aren't doing work so you probably won't get tired.
If your friend held the wagon still and you tied the cord around a tree and pulled it tight, the tree could exert the same force as you did. Do you think the tree would get tired? The tree can exert a force but can the tree do work?
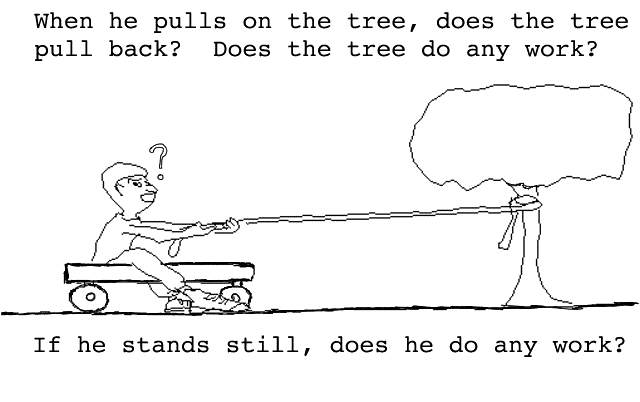
How much power can you develop?
You could run up a flight of stairs rapidly or you could climb the same stairs very slowly. Either way, you do the same amount of work because you apply the same force (equal to your weight) through the same distance (the height of the stairs.) Power is work per time. That is, if you do the same amount of work in a shorter time, it takes more power. Two cars might weigh the same and they might climb the same hill, hence they do the same amount of work. But if one of the cars is a clunkey old car and the other car is a powerful sports car, the sports car can climb the hill much faster because it has a more powerful engine. In this experiment we are going to see how many watts of power you can develop.
Finding the force you must exert. Every time you weigh yourself, you are measuring the force that the earth pulls down on you (this is called your weight) and you are also measuring how hard the scale pushes upward on the bottoms of your feet. If you weigh 80 pounds, the scale must push upward on you with exactly 80 pounds. Most people find it peculiar that the scale pushes upward on them when they weigh themselves, but it always will. If you weigh 80 pounds and are standing on the floor, the floor will push up on the bottoms of you feet with a force of 80 pounds. (This is very hard to understand but it is true--think of pressing the binder clip against the wall--what must the wall do to the binder clip? Isaac Newton was the first to understand this and his ideas about action and reaction forces have revolutionized the way we think.) The first thing you must do in this experiment is to weigh yourself. You will probably have to weigh yourself in pounds but your teacher will explain how you will convert this to the metric unit of force, the newton. (For example, an 80 pound person will also weigh 356 newtons, the metric unit of force.)
Measuring the distance you will climb. Your teacher will explain how to find the height of the stairs you will climb. This height will be in the metric unit of distance, the meter. Even through you will run up at an angle, you will only need to know the height you climb.

Computing the work you will do. Since work is force times the distance through which the force acts, you will find the amount of work you do in climbing the stairs by multiplying your weight in newtons by the height of the stairs in meters. Force measured in newtons, times distance measured in meters, gives the metric unit of work or energy, and it is called the joule. (For example if an 80 pound person climbs a flight of stairs which goes up one floor, this person will exert a force of about 360 newtons through a distance of about 4 meters, hence the person will do about 1440 joules of work.)
Measuring the time it takes for you to climb the stairs: Your teacher or another student will measure how much time in seconds it will take for you to climb the stairs. Run as fast as you can, skip stairs if you want to, pull on the hand rail if it helps but don't fall and hurt yourself! The faster you climb the stairs, the more power you will develop.
Computing the amount of power you develop: Power is the amount of work you do divided by the amount of time it took to do the work. The work you did in climbing the stairs is the force you applied (your weight) times the distance you moved upward (the height of the stairs.) That is:
Work (in joules) = your weight (in newtons) X the height of the stairs (in meters.)
Now the power you developed is the work you did divided by the time it took, or:
Power (in watts) = work (in joules) divided by the time (in seconds.)
If we call the time it took for you to climb the stairs in seconds, T, the height of the stairs in meters, h, your weight in newtons, W, then to find the power you developed in watts, P, the following formula restates what we said above:
P = W x h/t
Other questions to consider:
1) If a big person and a small person run up the stairs in the same time, which of them develops the most power?
2) If a big person and a small person run up the stairs in the same time, which of them does the most work?
3) Which person exerts the largest force on the stairs, the big person or the small person?
4) One horsepower is 746 watts. How would you find out how much horsepower you developed in running up the stairs? (Do it! That is, calculate your horsepower.)
5) Do you think a bicycle helps you to develop more power? (This is not easy--think about it.)
Back to Background Material on Force, Work and Power.
Back to Teaching Suggestions on Force, Work and Power.