The system to discretize
is replaced by the extended system
where 
, 
, 
, and 
are four
free additional parameters which will be used in the discretized
approximation, either to model a physical effect (some dispersion with
for example), either to adjust some numerical corrections or to
model a specific boundary condition. The variables E and 
are
defined by 
where 
and 
are the components propagating respectively forward and backward
along the axis, with identical definitions for B.
The discretized system takes the form
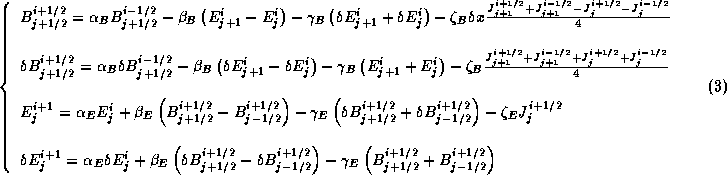
with
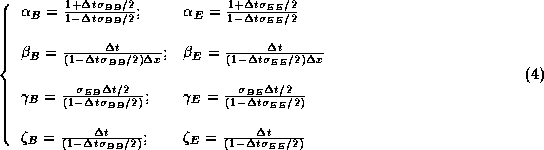
In practice, a numerical correction of the form 
. 
must be added to the first equation of the set
(2)in order to satisfy the static limit 
in vacuum.
For 
, the system
(2) reduces to
(1) because, in vacuum, we have 
and 
:
0, the
discretized system reduces to the standard FDTD approximation in vacuum (or in
a dispersive medium by tuning to a non-zero value);
,
the wave equation in vacuum is modeled with some additional numerical control
at the discretized level. A cut-off on the high frequencies is obtained and
can be tuned by the value of (cf. Fig.
1), giving the possibility to reduce the numerical noise associated with the
high frequencies as well as the numerical Cerenkov effect, which is caused by
the high frequencies.
For 
at a boundary, the system reduces
to the usual one-dimensional Sommerfeld outgoing-wave boundary condition and
is extended to the second order approximation of the Engquist and Majda
outgoing-wave boundary condition in higher dimension.
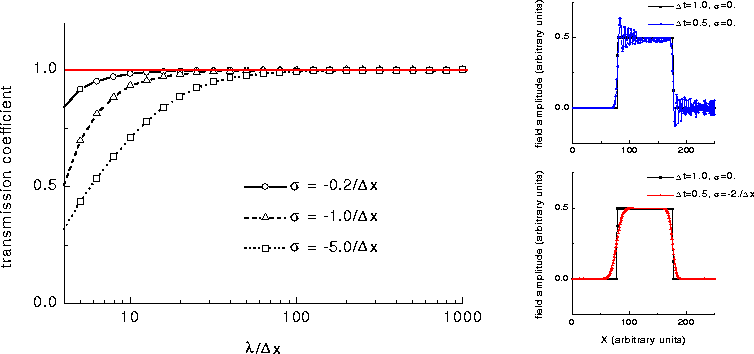
Figure 1: (when nonequal to zero) has an effect when using the
discretized form of the equations. On the left, it is shown that the short
wavelength waves ( 
is the mesh size) are damped when .
A benefit of this damping is a tunable reduction of numerical noise, has shown
on the right where the response of the system to a heavyside signal is
displayed for 
(top) and for 
(bottom).
