First it is instructive to see how this trap for magnetic dipoles doesn't work.
It is not enough to simply
stabilize the top/dipole against flipping. We can consider this the infinite
spin case, whether the stability against flipping is provided by spin or by some
mechanical arrangement. Assume the top's magnetic dipole moment 
is always
oriented in the vertically downward -z direction and the repulsive magnetic
field B from the base magnet is primarily in the vertically upward
+z direction in the levitation region. The potential energy U is
. There are two conditions
for stable levitation.
The lifting force 
must balance the
weight of the top mg
and the potential energy at the levitation point must be a minimum.
If the energy is a minimum
it must have positive curvature in every direction or
, where the 
are x, y,
and z. However,
at any point in free space so the energy minimum condition cannot be
satisfied in all directions. Instead of a minimum there is a saddle point.
This is just a consequence of the fact that the magnetic field
in the trapping region is divergence- and curl-free.
For completeness we note a second way that the trap does not work. We considered that the trap might work by strong focusing. If the top and/or base had non-uniform magnetization, the spinning might create the appropriate time-dependent force to be a stable solution of the Mathieu equation. Measurements of the nonuniformities, the top's inclination, and rotation showed that any focusing forces were too small by many orders of magnitude. Replacing the commercial square-magnetized base with a cylindrically symmetric ring magnet does not degrade the confinement at all, contrary to what one would expect if strong focusing was the trapping mechanism.
The gyroscopic action must do more than prevent the top from flipping. It must act to
continuously align the top's precession axis to the local magnetic field
direction (see figure 2).
Under suitable conditions,
the component of the magnetic moment along the local magnetic field direction is an
adiabatic invariant. When these conditions are met, the potential energy depends only
on the magnitude
of the magnetic field and gravity.
While each component of the magnetic field must satisfy Laplace's equation
(i.e. ), the magnitude of
the magnetic field does not. This allows the curvature of the potential energy
to be concave up (and not a saddle point) at the levitation height.
Properly understood, the trap mechanism is similar to magnetic gradient traps for neutral particles with a quantum magnetic dipole moment. Such traps were first proposed and used for trapping cold neutrons [10] and are currently used to trap atoms [11], including recent demonstrations of Bose-Einstein condensation. The spin magnetic moment of a particle such as a neutron along the magnetic field direction is an adiabatic invariant. If the field does not change too rapidly or go through zero allowing a spin flip, the spin magnetic moment along the magnetic field direction is constant. The potential energy then depends only on the magnitude of the magnetic field. Since localized magnetic field minima are allowed (isolated maxima are prohibited) by the laws of magnetostatics, a trap for anti-aligned dipoles is possible. Spin polarized particles or atoms seek the weak-field position in magnetic gradient traps.
Another example of a similar adiabatic invariant is the magnetic moment of a charged particle spiraling along a magnetic field line. Here again, if the field changes slowly, the magnetic moment due to the particle orbit perpendicular to the field is constant. A charged particle can be trapped in the low field part of a magnetic mirror.
We make two simplifying assumptions. First we assume that the
top is a magnetic dipole whose center is also the center of mass. The position of the
center of mass and the dipole are located at the same coordinates r.
Second, we assume the ``fast'' top condition
that the angular momentum
is along the spin axis of the top which also coincides with the magnetic moment
axis. (We relax the fast top condition in the computer simulation code described
in Appendix 2.) That is, the angular momentum
L
. Here I is the rotational inertia of the top around the spin axis,
is the constant angular spin frequency, and is the
magnetic moment. 
and is constant. The spin
can have a + or a - sign due to the two possible spin directions,
parallel or antiparallel to respectively.
The sense of the angular momentum doesn't effect the stability of the top, only
the sense of the precession.
The torque and force equations that describe the motion of the top
(ignoring air resistance and other losses) are
and
The magnetic field is a function of position B(r) and
the magnetic moment depends on both position and time
,t).
Equation (1) says that the top's spin axis rotates about the direction of the local magnetic
field B with an angular precession frequency
It is important to note that the precession frequency is inversely proportional to the spin
frequency. Although we have assumed that the top is ``fast'', if it is too fast, the
precession frequency will be too slow to keep the top oriented to the local magnetic field
direction. This is the origin of the upper spin limit.
Equation (1) also says that to lowest order, the component of the magnetic moment along the
local magnetic field
direction is a constant which we can call 
. We consider the case
shown in figures
1 and 2 where is antiparallel (repulsive orientation) to B.
The potential energy of the top is
We can expand the magnetic field around the levitation point as a power series for our
cylindrically symmetric geometry
where
and S and K are evaluated at the levitation point. This expansion uses the
curl and divergence equations, 
=0 and
=0, to write the field components in terms of 
and
its derivatives with respect to z.
The potential energy becomes
At the levitation point, the expression in the first curly braces
must go to zero. The magnetic field gradient balances
the force of gravity
if the ratio of the mass to the magnetic moment 
is correct. This ratio
is adjusted by adding small weights to the top. For the potential energy
to be a minimum at the trapping point, both K and 
must be positive.
The energy well is then quadratic in both r and z and approximates a harmonic oscillator potential.
Thus, the trapping condition at the levitation point is
If the magnetic moment was not free to orient to the local field direction as it moved off center (see
figure 2),
the term in the second curly
braces would be only 
, and the top would be unstable radially (for K>0).
The positive term in the second curly
braces represents the energy required to reorient the top's axis from vertical to the local field direction.
This reorientation energy creates the radial potential well at the levitation height when the trapping condition
in equation (10) is satisfied.
Figure (3) shows B, -S, K and 
for the field of a ideal
ring magnet of inner
diameter 6 cm and outer diameter 10 cm and shows
the trapping region. The trapping height and the stable region have been confirmed by experimental
measurements and computer simulation of the equations of motion. The trapping height is above the maximum
in the field and just above the inflection point
of where the curvature K turns positive. A correctly weighted but non-precessing
magnet would be stable in z but unstable in r at this point. Slightly below
the levitation point, the top will
fall but it is stable in r, which makes it possible to spin the top on the base
and raise it into position.
Figure (4) shows an experimental setup for measuring the upper spin limit. A white mark on the spinning top is sensed by the phototransistor and triggers pulses in a drive coil circuit. The phase of the drive is adjusted by rotating the drive coils around the base magnet. The synchronous electromagnetic drive can maintain the top spinning at a constant rate (countering air resistance) or, with increased amplitude, spin it faster. When the top exceeds the maximum stable spin rate it spirals out radially. Appendix (1) shows one way to calculate the upper spin frequency limit. The system is described by a set of linearized equations which are then solved. The reason for the upper spin limit is that the precession becomes too slow to allow the top to reorient to the local field direction as the top makes its radial excursion in the potential well. The adiabatic condition on the magnetic moment is violated and the energy no longer depends only on the magnitude of the magnetic field. The top becomes unstable in the radial direction.
The drive system shown in figure (4) couples to a residual transverse magnetization
in the small ring magnet that is part of the top. Other drive variations
also work including straight wires laid across the base magnet and a
rotating field made with coils driven 90
out of phase at around 20 Hz.
If the temperature
doesn't fluctuate too much, the driven systems can levitate indefinitely.
The lower spin limit for the top corresponds to the condition for a ``sleeping''
top. A sleeping
top is a fast top, that when started vertically, remains vertical. The
minimum speed required for a sleeping top
is given by the relation 
or
where 
is the effective radius for the moment of inertia
of the top and 
is the moment of inertia around an axis transverse
to the main spin axis.
For practical tops
the ratio of the moments of inertia is between 1 and 1/2. At the low frequency
limit the top tips over enough that the magnetic field gradient can no longer
support it and it falls.
A condition for the possibility of stable levitation is that the upper spin limit
must be higher than the lower spin limit.
While this sounds trivial, there is no guarantee that for realizable systems the
maximum frequency
is not below the minimum. From appendix (1) equation (17)
and equation (11)
we can get an expression for the ratio of the maximum to minimum spin frequency.
For tops that are nearly all magnetic material, the ratio 
is
essentially a material property, the magnetic moment per unit mass.
For the materials and configuration used with some of our homemade tops
the permissible spins were measured to be in the range of 1,000 to 3,000 rpm.
and the undriven float time as much as 4 minutes in air.
Attempts to achieve longer levitation by
spinning the top faster run into trouble with the upper spin limit.
Measurements on top parameters were made and compared with the
analytical theory and a computer simulation of the top motion. The computer
simulation does not make the fast top approximation that all
the angular momentum is along the top axis and follows the full
rotational dynamics. The equations used in the simulation are described
in Appendix 2. The simulation monitors the top center of mass in
x, y, and z, the projection of the top spin axis on the x-y plane, and
as the spin frequency is
slowly ramped. One can clearly see the top start
to go unstable when the component of along B begins
to change near the upper spin frequency limit. The simulation
can investigate both the upper and lower stability bound.
We describe here how some of the top parameters were measured for the commercial
Levitron top and an experimental stemless top on both the
Levitron base magnet as well as an adjustable experimental circular base magnet.
The stemless top was developed
so that its rotational inertia could be more accurately determined by geometry
alone. Instead of using weights, adjustment is achieved by changing the spacing
between two ring magnets that make up the base.
The rotational inertia of the Levitron top, with weights, was determined
by a torsion wire method. The earth's field had to be cancelled with another
magnet and the wire torsional spring constant was calibrated with known
spheres. The
magnetic moments of the tops were determined with a compass needle aligned
with the earth's field and a
calibrated coil. The top dipole caused a deflection of the compass needle which was
nulled out by a current through the coil. From this current the dipole
moment could be determined more accurately than from gaussmeter measurements
alone.
The field gradient S at the levitation point was determined
from equation (9).
A technique similar to NMR was used to find the
precession frequency 
and the bounce frequency 
described in appendix 1. First, the top was driven at a constant frequency
with the system shown in
figure 4.
A small drive coil was arranged to couple to either the
precession or the axial bounce motion and then pulsed, to drive the mode.
The resulting oscillation was then sensed by the same coil and
fed to a narrow band amplifier and frequency counter. could
be measured to about
1% accuracy while could only be measured to within 10% due to
coupling between the axial and radial oscillations. 
and K were
then determined from equations (3) and (14). Hall gaussmeter measurements
of , S, and K were in reasonable agreement with the above
method but are considered less accurate.
Below we present a table of values for three of the cases we measured
and compared to the linear theory and the computer simulation. In general,
the experimental results agree with the theory and simulation to within
20%. In most cases, the experiment doesn't reach the calculated
upper frequency
limit and in all cases, doesn't quite reach the lower frequency limit.
We believe that there could be errors in our value for
. While we can measure the precession frequency
very precisely at any spin frequency , we
found that our calculation of depended on the spin frequency
in a way which we don't fully understand yet. Errors in affect the
calculation of the upper and lower spin limits. It is also worth mentioning
here that the top is not really a point dipole, but a large (compared to
the potential well) ring magnet. To do a better job, one should integrate
over the whole magnet.
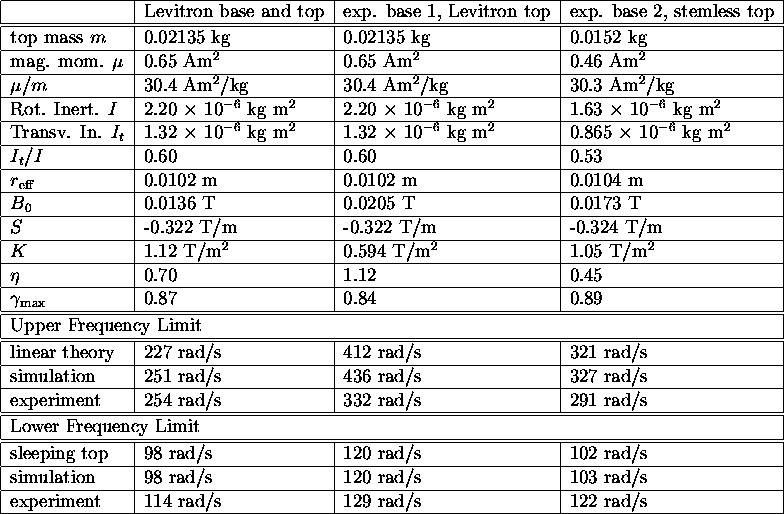
Table 1: Measured and computed values for three different top-base
configurations
The depth of the energy well can be estimated from the observed bounce frequency in the
well, about 1 Hz, and the excursion amplitude, about 5 mm. The well depth is
on the order of 
joules.
If we were trying to trap a 20 gram top in a gravitational well of the same
depth we would be trying to catch it in a depression only 50 microns deep.
This limits how much translational energy the top can have when trying to
insert it into the levitation region.
One mysterious feature of the Levitron has been the need to constantly adjust the weight
of the top, even over a period of a few minutes. Our experiments showed that this was due
to temperature variation due to handling and ambient temperature changes. The
ceramic magnets used have a reversible demagnetization temperature coefficient of
about 0.2% per C. Cooling the magnets increases their field strength and requires the
top to be heavier to levitate.