Coherent Diffractive Imaging (CDI)
Recent years have witnessed two revolutionary developments in X-ray science. First, a new approach to X-ray crystallography, known as CDI, was first demonstrated in 1999 (1) that allows structural determination of non-crystalline specimens and nano-crystals with a resolution limited only by the spatial frequency of the diffracted waves. Second, large-scale coherent X-ray sources, such as XFELs and diffraction-limited storage rings, have been under rapid development worldwide. Furthermore, tabletop coherent X-ray sources based on HHG have advanced rapidly, significantly increasing access to ultrafast coherent X-ray beams for applications in nano and materials science. In recent years, the combination of powerful coherent X-ray sources and CDI methods, coupled with advanced X-ray detectors and computational algorithms, has opened up new research frontiers in the physical and biological sciences that are not attainable with conventional X-ray crystallography (2-5).
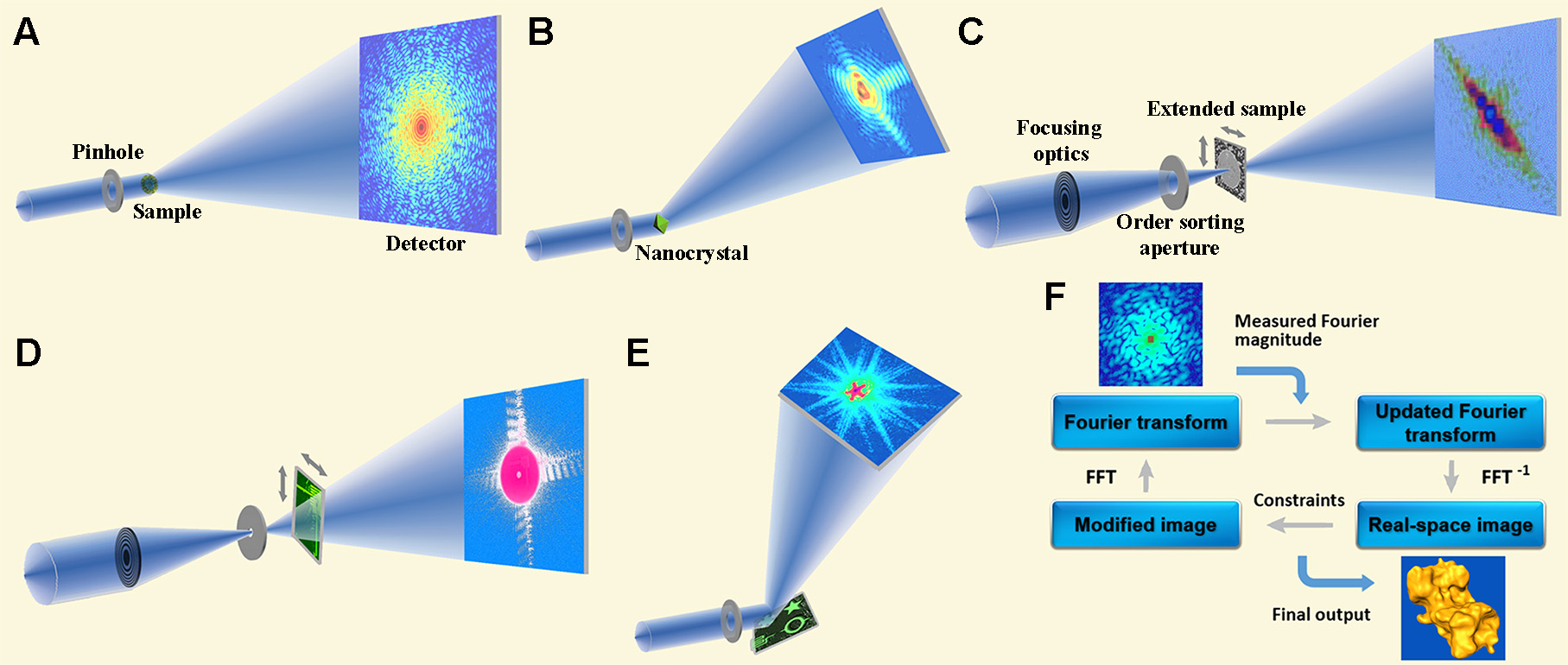
In CDI, a coherent wave illuminates an object and the diffracted wave field in the far-field is proportional to the Fourier transform of the object. While the magnitude squared of the Fourier transform can be measured as an intensity by a detector, the phase information is lost, which constitutes the well-known phase problem. For a non-crystalline specimen or nano-crystal, the diffraction pattern is continuous and can be sampled at a frequency finer than the Nyquist interval. When the number of independently sampled intensity points is larger than the number of unknown variables associated with a specimen, the phase information is in principle encoded inside the diffraction intensity (6) and can be retrieved by iterative algorithms (7). Over the years, various CDI methods have been developed, including plane-wave CDI, Bragg CDI, ptychography, reflection CDI, Fresnel CDI, and sparsity CDI. These CDI methods have been used to study a broad range of samples in physics, chemistry, materials science, nanoscience, geology, and biology (2-5).

Selected Publications
1. J. Miao, P. Charalambous, J. Kirz and D. Sayre, "Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens", Nature 400, 342-344 (1999).
2. J. Miao, T. Ishikawa, I. K. Robinson and M. M. Murnane, "Beyond crystallography: Diffractive imaging using coherent x-ray light sources", Science 348, 530-535 (2015).
3. M. Gallagher-Jones, J. A. Rodriguez and J. Miao, "Frontier Methods in Coherent X-ray Diffraction for High-Resolution Structure Determination", Q. Rev. Biophys. 49, e20 (2016).
4. I. Schlichting and J. Miao, "Emerging opportunities in structural biology with X-ray free-electron lasers", Curr. Opin. Struct. Biol. 22, 613–626 (2012).
5. J. Miao, R. L. Sandberg and C. Song "Coherent X-ray Diffraction Imaging", IEEE J. Sel. Top. Quant. Electron. 18, 399-410 (2012).
6. J. Miao, D. Sayre and H. N. Chapman, "Phase Retrieval from the Magnitude of the Fourier transform of Non-periodic Objects", J. Opt. Soc. Am. A. A 15, 1662-1669 (1998).
7. Y. Shechtman, Y. C. Eldar, O. Cohen, H. N. Chapman, J. Miao and M. Segev, "Phase Retrieval with Application to Optical Imaging: A contemporary overview", IEEE Signal Processing Mag. 32, 87-109 (2015).